Страхование и полезность (1.3)

В разд. 1.2 , чтобы лучше понять экономическую роль страхования, мы описали теорию полезности. Начнем анализ этой роли с одного примера. Предположим, что лицо, принимающее решения, владеет собственностью, которая может быть повреждена или уничтожена в течение следующего отчетного периода. Величина ущерба, которая может равняться 0, - это случайная величина, которая будет обозначаться через X. Мы будем предполагать, что ее распределение известно. Тогда величина E[X], ожидаемая величина ущерба в следующий отчетный период, может рассматриваться как долговременные средние потери, если эксперимент, состоящий в том, что собственность подвергается опасности ущерба, может многократно проводиться при неизменных условиях. Ясно, что одно лицо, принимающее решения, не может осуществить такую длительную последовательность экспериментов.

Предположим, что создается страховая организация (страховщик), цель которой - уменьшить финансовые последствия повреждения или уничтожения собственности. Страховщик выпускает контракты (договоры), которые являются обязательствами выплатить владельцу собственности определенную сумму (страховую сумму), равную или меньшую, чем понесенные финансовые потери, если собственность повреждена или уничтожена в течение периода действия договора. Платежи, обусловленные этими обстоятельствами и связанные с размером ущерба, называются страховыми выплатами. В обмен на обязательства, закрепленные в договоре, владелец собственности (страхователь) выплачивает страховщику вознаграждение (премию).

Величина премиальных выплат определяется принципом экономических решений, которые принимаются как страховщиком, так и страхователем. Существует возможность взаимовыгодного страхового договора, когда величина премии по договору, определяемая страховщиком, меньше, чем максимальная сумма, которую владелец собственности готов платить за страхование.

При целом ряде финансовых обстоятельств для отдельно взятого договора страхования функция полезности страховщика может приближаться прямой линией. В этом случае при определении размера премии страховщик должен руководствоваться принципом ожидаемого значения, как указано в утверждении 3 разд. 1.2. Другими словами, страховщик должен назначить в качестве базовой премии при полном страховом покрытии величину, равную ожидаемому ущербу, E[X] = μ. В этом контексте μ называется нетто-премией для страхового договора, заключенного на один срок.

Для того чтобы обеспечить себе средства на покрытие расходов и уплату налогов, а также некоторую прибыль и чтобы до некоторой степени обезопасить себя от неблагоприятной динамики потерь, страховая система должна при определении премии по договору установить надбавку, которая прибавляется к нетто-премии. Например, премия с надбавкой, обозначаемая через H, может задаваться равенством

H = (1 + а) μ + с,      а > 0, с > 0.

Можно считать, что величина aμ в этом соотношении связана с теми расходами, которые изменяются с изменением ожидаемого ущерба, и с риском того, что реальные страховые выплаты будут отличаться от ожидаемых. Константа с соответствует ожидаемым расходам, которые не зависят от величины ущерба. Ниже мы рассмотрим другие экономические принципы, лежащие в основе определения премий, которые могут быть приемлемыми для страховщика.

Применение теории полезности

Применим теорию полезности к проблеме принятия решений, с которой сталкивается лицо, собственность которого подвергается риску. Такой владелец собственности обладает функцией полезности капитала u(w), где капитал w измерен в денежных единицах. Он может понести потери из-за наступления случайных событий, которые нанесут вред его собственности. Распределение случайных потерь X предполагается известным. Как и в (1.2.1 ), владельцу собственности безразлично, платить ли сумму G страховщику, перекладывая на него случайные финансовые потери, или принимать риск на себя. Это положение может быть формализовано соотношением

u(w - G) = E[u(w - X)]. (1.3.1)

Правая часть формулы (1.3.1) представляет собой ожидаемую полезность при отказе от покупки страхового договора, если текущая величина капитала владельца собственности равна w. Левая часть представляет собой ожидаемую полезность при выплате суммы G за полное финансовое покрытие.

Если функция полезности владельца является возрастающей и линейной, т. е. u(w) = bw + d, b > 0, то он примет принцип ожидаемого значения. В этом случае владелец собственности или не отдает предпочтение ни одной из возможностей, или отдает предпочтение страхованию, если

u(w - G) - b(w - G) + d ≥ E[u(w - X)] = E[b(w - X) + d],
b(w - G) + d ≥ b(w - μ) + d,
G ≤ μ.

Таким образом, если функция полезности владельца собственности возрастает и линейна, величина премии, при которой он не отдает предпочтения ни одной из возможностей или предпочитает приобрести полное страховое покрытие, не превосходит величины ожидаемых потерь. При отсутствии дотаций при долгосрочном планировании страховщик должен позаботиться о том, чтобы полученные премии превысили его ожидаемые потери. Поэтому в рассматриваемом случае заключение взаимовыгодного страхового договора маловероятно. При заключении страхового договора страховщик, для того чтобы избежать недостаточности поступлений, должен назначить премию, размер которой превышает ожидаемый ущерб и расходы. Таким образом, функция полезности владельца собственности не может быть линейной.

В разд. 1.2 отмечалось, что для существования функции полезности необходимо, чтобы предпочтения лица, принимающего решения, обладали определенными свойствами согласованности. Хотя эти требования и не были перечислены, отметим, что они не содержат никаких положений, в силу которых функция полезности оказывалась бы линейной, квадратичной, показательной, логарифмической или имела какую-либо другую определенную форму. На самом деле каждая из перечисленных выше функций может служить функцией полезности для некоторого лица, принимающего решения, а функция, составленная из их сегментов, может отражать предпочтения еще какого-то лица.

Все же кажется естественным предполагать, что u(w) является возрастающей функцией, «больше - лучше». Кроме того, было замечено, что для многих лиц, принимающих решения, при увеличении капитала равными долями полезность увеличивается уменьшающимися долями. Это отражается в известном экономическом положении об убывающей предельной полезности.

Приближение функции полезности на рис. 1.2.1 состоит из сегментов прямых с положительными коэффициентами наклона. Это дает соотношение ∆²u(w) ≤ 0. (По поводу конечных разностей см. приложение 5.) Если это наблюдение распространить на более гладкие функции, то мы придем к следующим двум свойствам: u'(w) > 0 и u''(w) < 0. Из второго неравенства следует, что u(w) является строго выпуклой вверх функцией.

В обсуждении решений, принимаемых в страховании на основе строго выпуклой вверх функции полезности, мы будем пользоваться неравенством Иенсена. Это неравенство утверждает, что для с. в. X и функции u(w)

если u'' < 0, то E[u(X)] ≤ u(E[X]), (1.3.2)

если u'' > 0, то E[u(X)] ≥ u(E[X]). (1.3.3)

Неравенство Иенсена предполагает существование обоих математических ожиданий. Одно из доказательств этого неравенства составляет упр. 1.3. Другое доказательство неравенства (1.3.2) почти сразу следует из анализа приведенного ниже рис. 1.3.1.

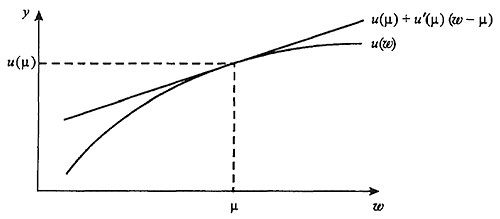
Рис. 1.3.1. Доказательство неравенства Иенсена
в случае u'(w) > 0 и u"(w) < 0.

Если E[X] = µ существует, рассмотрим касательную к u(w) в точке (µ,u(µ)),

y = u(µ) + u'(µ) (w - µ).

Из-за строгой выпуклости вверх функции u(w) ее график будет лежать ниже касательной. Другими словами,

u(w) ≤ u(µ) + u'(µ)(w - µ)    (1.3.4)

для всех значений w. Если вместо w подставить случайную величину X и взять математическое ожидание от обеих частей неравенства (1.3.4), то мы получим E[u(X)] ≤ u(µ).

Это основное неравенство имеет ряд применений в актуарной математике. Применим неравенство Иенсена (1.3.2) к задаче принятия решения о страховании, сформулированной в виде формулы (1.3.1). Мы будем предполагать, что предпочтения лица, принимающего решения, таковы, что u'(w) > 0 и u''(w) < 0. Применяя неравенство Иенсена к формуле (1.3.1), мы имеем

u(w - G) = E[u(w - X)] ≤ u(w - µ).    (1.3.5)

Поскольку u'(w) > 0, u(w) является возрастающей функцией. Поэтому из неравенства (1.3.5) следует, что w - G ≤ w - µ или G ≥ µ, причем G > µ, если только с.в. X не является константой. В экономических терминах, мы установили, что если u'(w) > 0 и u''(w) < 0, то принимающий решения будет платить за страхование сумму, превосходящую ожидаемые потери. Если величина G не меньше премии, назначенной страховщиком, то возможен взаимовыгодный страховой договор.

Формально, будем говорить, что лицо, принимающее решения на основе функции полезности u(w), не склонно к риску, тогда и только тогда, когда u''(w) < 0.

Займемся теперь общей функцией полезности для страховщика. Обозначим через u_I(w) функцию полезности страховщика и через w_I текущий капитал страховщика в денежных единицах. Тогда минимальная допустимая премия H за взятый на себя риск X с точки зрения страховщика может быть определена из формулы

u_I(w_I) = Е[u_I(w_I + H - X)].      (1.3.6)

Ее левая часть является полезностью, соответствующей текущему положению страховщика. Правая часть является ожидаемой полезностью, соответствующей получению премии H и выплате случайных потерь X. Другими словами, для страховщика нет различия между его текущим положением и предоставлением страхового покрытия от риска X при условии получения премии H. Если функция полезности страховщика такова, что u'_I(w) > 0 и u''_I(w) < 0, то, воспользовавшись неравенством Иенсена (1.3.2) и соотношением (1.3.6), мы можем получить

u_I(w_I) = Е[u_I(w_I + H - X)] ≤ u_I(w_I + H - µ).

Применяя те же рассуждения, что и для формулы (1.3.5), мы видим, что H ≥ µ. Если величина G, определяемая лицом, принимающим решения, исходя из соотношения (1.3.5), такова, что G ≥ H ≥ µ, страховой договор может быть заключен. Это означает, что ожидаемая полезность ни для одной из сторон не убывает.

Функция полезности основана на предпочтениях лица, принимающего решения, при различных распределениях исходов. Страховщик - это не обязательно отдельное физическое лицо. Это может быть товарищество, акционерное общество или государственная организация. В этом случае определение u_I(w), функции полезности страховщика, может оказаться довольно тяжелой задачей. Например, если страховщик является акционерным обществом, одной из обязанностей правления является выработка логически последовательного множества предпочтений относительно ряда рискованных предприятий. Эти предпочтения могут включать компромиссы между не совпадающими позициями по отношению к риску разных групп акционеров.

Для иллюстрации свойств функций полезности используется ряд элементарных функций. Мы рассмотрим сейчас показательную, степенную с дробным показателем и квадратичную функции. Примеры 1.6, 1.8, 1.9, 1.10(b) и 1.13 относятся к логарифмической функции полезности.

Показательная (или, иначе, экспоненциальная) функция полезности имеет вид

u(w) = -e^-aw для всех w и для некоторого фиксированного а > 0 и обладает рядом привлекательных свойств.

Во-первых,

u`(w) = ae^-aw > 0.

Во-вторых,

u``(w) = -а²е^-aw < 0.

Поэтому u(w) может использоваться в качестве функции полезности для лица, не склонного к риску. В третьих, заметив, что

Е[-е^-аX] = -E[е^-аХ] = -M_x(-а),

мы, по сути дела, нашли производящую функцию моментов с.в. X. В предыдущей формуле

M_x(t) = E[e^tX]

обозначает производящую функцию моментов с.в. X. В четвертых, страховые премии не зависят от капитала лица, принимающего решения. Для проверки этого утверждения следует подставить показательную функцию полезности в формулу (1.3.1). Тогда

-e^-a(w-G) = E[-e^-a(w-X)],  e^aG = M_x(a),    G = lnM_x(a) / a

и G не зависит от w.

Проверка для страховщика осуществляется подстановкой показательной функции полезности с параметром а_I в (1.3.6):

-e^-a_Iw_I = E[-e^{-a_I(w_I + H- X)}],  e^a_Iw_I = -e^{-a_I(w_I + H)} M_x(a_I),  H = lnM_x(a_I) / a_I

Пример 1.3.1.

Функция полезности лица, принимающего решения, имеет вид u(w) = -e^-5w. Для принимающего решения имеется две случайные экономические возможности. Первая из них, обозначаемая через X, имеет нормальное распределение со средним 5 и дисперсией 2. Впредь, говоря о нормальном распределении со средним µ и с дисперсией o², мы будем пользоваться сокращенной записью N(µ, o²). Другая возможность, обозначаемая через Y, имеет распределение N(6, 2,5). Какую возможность следует предпочесть?

Решение. Имеем

E[u(X)] = Е[-e^-5X] = -M_X(-5) = -e^{[-5(5)+(52)(2)/2]} = -1,

E[u(Y)] = Е[-e^-5Y] = -M_Y(-5) = -e^{[-5(6)+(52)(2,5)/2]} = -е^1,25.

Таким образом,

E[u(X)] = -1 > E[u(Y)]  = -е^1,25,

и распределение с.в. X предпочтительнее распределения с.в. Y.

В примере 1.3.1 с.в. X предпочтительнее, чем X, несмотря на то, что µx = 5 < µy = 6. Поскольку принимающий решения не склонен к риску, тот факт, что распределение с.в. Y более «размазано», чем распределение с.в. X, свидетельствует против распределения с.в. Y при оценке его желательности. Если с.в. Y имеет распределение N(6, 2,4), то Е[u(Y)] = -1 и для принимающего решения будет безразлично, выбрать распределение X или распределение Y.

Семейство степенных с дробным показателем функций полезности задается соотношением

u(w) = w^γ,   w > 0,   0 < γ < 1.

Элемент этого семейства может представлять предпочтение лица, не склонного к риску, поскольку

u`(w) = γw^γ-1 > 0   и   u``(w) = γ (γ - l)w^γ-2 < 0.

Для этого семейства размер премии зависит от капитала лица, принимающего решения, достаточно реалистичным во многих ситуациях образом.

Пример 1.3.2.

Функция полезности лица, принимающего решения, задается выражением u(w) - √w. Принимающий решения имеет капитал w = 10 и может понести случайные потери X, которые распределены равномерно на интервале (0,10). Какую максимальную сумму он готов заплатить за полное страховое покрытие против указанных случайных потерь?

Решение. Подставляя указанное выражение для функции полезности в (1.3.1), мы получим

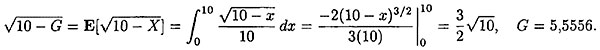
Принимающий решения не склонен к риску и u'(w) > 0. Согласно обсуждению формулы (1.3.5), следует ожидать, что G > Е[Х], и в нашем примере G = 5,5556 > Е[Х] = 5.

Семейство квадратичных функций полезности задается соотношением

u(w) = w - aw²,   w < (2а)^-1,    a > 0.

Элемент этого семейства может представлять предпочтение лица, не склонного к риску, поскольку u"(w) = -2а. Хотя квадратичная функция полезности удобна тем, что зависит только от первых двух моментов распределений рассматриваемых исходов, ряд последствий ее использования некоторым лицам кажется неразумным. Пример 1.3.3 иллюстрирует одно из таких последствий.

Пример 1.3.3.

Функция полезности лица, принимающего решения, задается выражением

u(w) = w - 0,01w²,   w < 50.

Принимающий решения сохранит капитал w с вероятностью p и будет нести финансовые потери величины с c вероятностью 1 - р. Для значений w, c и p, указанных в приведенной ниже таблице, найдем максимальную страховую премию, которую принимающий решения готов заплатить за полное страховое покрытие. Предположим, что с ≤ w < 50.

Решение. Для нашей задачи формула (1.3.1) приобретает вид

u(w - G) = pu(w) + (1 - p)u(w - c),

(w - G) - 0,01(w - G)² = p(w - 0,01w²) + (1 - p)[(w - c) - 0,001(w - c)²].

Для заданных значений w, p и c эта формула становится квадратным уравнением. Ниже приведены два его решения.

В примере 1.3.3, как и ожидалось, G превосходит величину ожидаемых потерь, 5. Однако максимальная страховая премия за потери с одним и тем же распределением растет с ростом капитала лица, принимающего решения. Этот результат кажется неестественным тем, кто считает, что более типичным поведением было бы уменьшение суммы, которую принимающий решения готов выплачивать за страхование, поскольку при увеличении капитала он мог бы позволить себе больший риск.

К сожалению, рост максимальной страховой премии с ростом капитала является характеристической чертой квадратичной функции полезности. Поэтому тем из принимающих решения лиц, которые полагают, что их способность брать на себя случайные потери растет с ростом капитала, не следует выбирать такие функции полезности.

Если мы рассмотрим пример 1.3.3, используя показательную функцию полезности, то, как мы знаем, премия G не будет зависеть от w, величины капитала. Так, если u(w) = -е^-0,01w, то можно показать, что G = 5,12 как при w = 10, так и при w = 20.

Пример 1.3.4.

Вероятность того, что собственности не будет нанесен ущерб за следующий период времени, равняется 0,75. Функция плотности возможных положительных потерь задается соотношением

f(x) = 0,25(0,01е^-0,01x),    х > 0.

Функция полезности владельца собственности имеет вид

u(w) = -e^-0,005w.

Вычислим ожидаемые потери и максимальный размер страховой премии, которую владелец собственности готов заплатить за полное страховое покрытие.

Решение. Ожидаемые потери задаются формулой

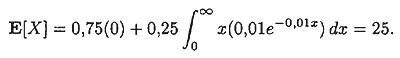
Применяем формулу (1.3.1) для определения максимальной премии, которую владелец собственности готов заплатить за полное страховое покрытие. Эта премия будет согласована с предпочтениями владельца собственности, выраженными такой функцией полезности:

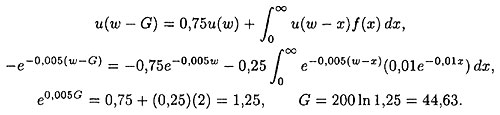
Таким образом, в соответствии с предпочтениями владельца собственности для покупки страхового договора, покрывающего все потери следующего временного периода, он готов выплатить сумму, превышающую ожидаемые потери, самое большее, на 44,63 - 25 = 19,63.

В примере 1.3.5 мы вводим понятие страхования, при котором сумма покрытия меньше, чем величина полных потерь. Формулу (1.3.1) можно модифицировать так, чтобы она годилась для случая, когда потери делятся между лицом, принимающим решения, и системой страхования.

Пример 1.3.5.

Владельцу собственности из примера 1.3.4 предлагается договор страхования, по которому будет выплачиваться 1/2 от любых потерь, понесенных им в следующем временном периоде. Ожидаемое значение частичных выплат в связи с потерями составляет Е[Х/2] = 12,50. Рассчитаем максимальную премию, которую владелец собственности выплатит за такой страховой договор.

Решение. Как показывает функция полезности, премия, согласованная с отношением владельца собственности к риску, определяется из соотношения

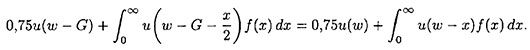
Левая часть этого равенства представляет ожидаемую полезность с частичным страховым покрытием. Правая представляет ожидаемую полезность при полном отсутствии страхования. Для показательной функции полезности и для функции плотности потерь из примера 1.3.4 можно показать, что G - 28,62. При частичном страховом возмещении владелец собственности готов заплатить сумму, превышающую ожидаемые частичные потери, самое большее, на величину G - µ = 28,62 - 25,50 = 16,12.