Теория полезности (1.2)

Если бы люди могли предсказать заранее последствия своих решений, их жизнь была бы более простой, но менее интересной. Мы все принимаем решения, основываясь на предпочтениях, которые отдаем некоторым последствиям. Однако мы не обладаем даром абсолютного предвидения. При самом лучшем исходе мы можем выбрать действие, которое приведет нас к одному множеству неопределенностей, а не к другому. Подробно разработана теория, которая помогает принять правильное решение перед лицом неопределенности. Эта область знаний называется теорией полезности. В силу большой значимости этой теории для страховых систем мы дадим здесь обзор основных ее положений.

Один из подходов к решению задачи принятия решения перед лицом неопределенности состоит в том, чтобы определить ценность экономического проекта со случайным исходом как его среднее, ожидаемое, значение. Согласно этому принципу ожидаемого значения, распределение возможных исходов можно заменить в целях принятия решения одним единственным числом, ожидаемым значением случайного исхода, выраженным в денежной форме. Согласно этому принципу, лицу, принимающему решения, должно быть безразлично, принять на себя случайные потери X или выплатить величину E[Х] с тем, чтобы обезопасить себя от возможных потерь. Аналогично, лицо, принимающее решения, должно быть согласно выплатить сумму, не превышающую величины Е[Y], для того чтобы принять участие в рискованном предприятии со случайными выплатами Y. В экономике ожидаемое значение случайных событий, которые сопряжены с денежными выплатами, часто называется честной или актуарной стоимостью этого события.

Многие из лиц, принимающих решения, не признают принцип ожидаемого значения. Они считают, что на принимаемое ими решение оказывают влияние размер их капитала и другие характеристики распределения исходов.

Ниже приводится пример, цель которого - продемонстрировать неадекватность принципа ожидаемого значения с точки зрения лица, принимающего решения в страховании от несчастных случаев. Во всех случаях предполагается, что вероятность наступления несчастного случая равна 0,01, а вероятность ненаступления несчастного случая равна 0,99. В зависимости от величины ущерба в результате наступления несчастного случая рассматриваются три варианта; ожидаемый ущерб для каждого из них приведен в следующей таблице:

Возможно, ущерб размера 1 мало волнует человека, принимающего решения, а значит, он может не пожелать платить сумму, большую, чем величина ожидаемого ущерба, за приобретение страхового покрытия. Однако ущерб в размере 1 000 000, который может превышать имеющиеся у него средства, оказался бы катастрофическим. В этом случае человек, принимающий решения, мог бы согласиться заплатить за страхование больше, чем сумма ожидаемых потерь, которая составляет 10 000. Тот факт, что сумма, которую принимающее решения лицо готово заплатить за страховое покрытие, может отличаться от ожидаемого значения, наводит на мысль, что для модели поведения принцип ожидаемого значения не подходит.

Для того чтобы объяснить, почему лицо, принимающее решения, может согласиться платить больше, чем ожидаемое значение, мы исследуем другой подход. Сначала мы просто предположим, что то значение полезности, которое рассматриваемое лицо связывает с капиталом величины w, измеренной в долларах, может быть выражено в виде некоторой функции u(w), называемой функцией полезности (капитала). Мы проведем процедуру, которая позволяет определить ряд значений такой функции. Для этого мы предположим, что лицо, принимающее решения, имеет капитал 20 000. Линейное преобразование

u*(w) = au(w) + 6, а > 0,

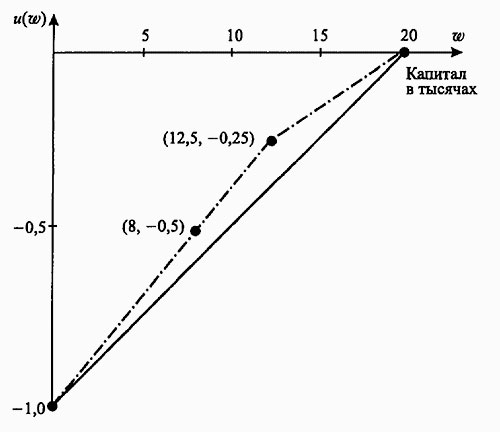
определяет функцию u*(w), которая по существу эквивалентна функции u(w). Тогда с помощью выбора чисел а и b мы можем произвольным образом определить значение функции полезности, соответствующей предпочтениям лица, принимающего решения, в точке 0 и еще в одной точке. Итак, мы полагаем u(0) = -1 и u(20 000) = 0. Эти значения отмечены на сплошной линии, изображенной на рис. 1.2.1.

Рис. 1.2.1. Определение функции полезности.

Рассмотрим теперь вопрос, волнующий лицо, принимающее решения, о котором шла речь выше: предположим, оно понесет потери величины 20 000 с вероятностью 0,5, с одной стороны, и останется со своим исходным капиталом с вероятностью 0,5, с другой стороны. Какова максимальная сумма G (размер премии в страховой литературе принято обозначать заглавной буквой, хотя это не случайная величина), которую это лицо согласилось бы заплатить за полное страховое покрытие случайных потерь? Мы можем формализовать этот вопрос следующим образом:

для какого значения G

u(20000 - G) = 0,5u(20 000) + 0,5 u(0) = (0,5)(0) + (0,5)(-1) = -0,5?

Если выплачивается сумма G, капитал, безусловно, сократится до величины 20 000 - G. Знак равенства здесь говорит о том, что лицо, принимающее решения, одинаково относится к тому, чтобы заведомо выплатить сумму G, и к тому, что ожидаемая полезность капитала будет такой, как в правой части выписанного выше соотношения.

Предположим, что ответ лица, принимающего решения, будет G = 12 000. Тогда

u(20 000 - 12 000) - u(8 000) = -0,5.

Этот результат изображен на пунктирной линии на рис. 1.2.1 . Возможно, наиболее важный аспект такого ответа состоит в том, что лицо, принимающее решения, согласно заплатить за страхование сумму, которая превосходит

(0,5) (0) + (0,5) (20 000) = 10 000,

ожидаемую величину потерь.

Эту процедуру можно использовать для добавления стольких точек (w,u(w)) при 0 ≤ w ≤ 20 000, сколько необходимо для получения удовлетворительного приближения к функции полезности капитала. Если установлены значения функции полезности для двух величин капитала w₁ и w₂, где 0 ≤ w₁ ≤ w₂ ≤ 20 000, то можно определить дополнительную точку, задав принимающему решения следующий вопрос: какую максимальную сумму он готов платить за полное страховое покрытие риска, что он останется с капиталом w₂ с некоторой вероятностью р, или с меньшим капиталом w₁ с вероятностью 1-р? Мы просим принимающего решения определить такое значение G, что

u(w₂ - G) - (1 - p)u(w₁) + p u(w₂). (1.2.1 )

Если его устраивает значение w₂ - G = w3, то точка (w₃, (1 - p) u (w₁) + p u(w₂)) принимается в качестве еще одной точки графика функции полезности. Этот процесс используется для нахождения четвертой точки (12 500, -0,25) на графике, изображенном на рис. 1.2.1 . Такое выяснение предпочтений дает множество точек на графике функции полезности лица, принимающего решения. По этим точкам можно построить гладкую функцию, которая имеет вторую производную, и принять ее в качестве функции полезности в каждой точке.

После того как принимающий решения определил свою функцию полезности, применяя описанный выше метод, эта функция может применяться для сравнения двух случайных экономических исходов. Эти исходы будут обозначаться случайными величинами (часто для термина «случайная величина» мы будем использовать сокращение с.в.) X и Y.

Мы ищем такое правило принятия решения, которое будет согласовано с предпочтениями, уже выявленными при определении функции полезности капитала. Так, если принимающий решения имеет капитал w и должен сравнить случайные исходы X и Y, то он выберет X, если

Е[u(w + X)] > Е[u(w + Y)],

и ему будет безразлично, какой из исходов X и Y осуществится, если

Е[u(w + X)] = Е[u(w + Y)].

Хотя метод опроса и использования функции полезности может показаться разумным, ясно, что наши неформальные построения должны быть подкреплены более строгой цепочкой рассуждений, если мы хотим, чтобы теория полезности составила логически последовательную и исчерпывающую основу для принятия решений перед лицом неопределенности. Если мы хотим понять экономическую роль страхования, такая основа необходима. Ниже приводится описание такой более строгой теории.

Отправной точкой теории является предположение о том, что разумный человек, сталкиваясь с двумя распределениями исходов, влияющих на капитал, сумеет выразить либо предпочтение по отношению к одному из этих распределений, либо одинаковое отношение к обоим. Далее, предпочтения должны удовлетворять некоторым требованиям согласованности. Наивысшей точкой теории является теорема, утверждающая, что если предпочтения удовлетворяют требованиям согласованности, то существует функция полезности u(w), такая, что если распределение X предпочтительнее, чем распределение Y, то Е[u(Х)] > Е[u(Y)], а если принимающий решения не отдает предпочтение ни одному из этих распределений, то Е[u(Х)] = Е[u(Y)]. Таким образом, качественное предпочтение или отсутствие такового можно заменить сравнением чисел. В разд. 1.6 даны ссылки на публикации, содержащие подробное изложение этой теории.

Перед тем как переходить к приложениям теории полезности в страховании, выпишем ряд утверждений, касающихся полезности.

Утверждения.

1. Теория полезности основана на предположении о существовании и согласованности предпочтений относительно распределений вероятностей возможных исходов. Функция полезности не должна отражать никаких неожиданностей. Она является численным описанием имеющихся предпочтений.

2. Функция полезности не должна, а на самом деле не может, определяться единственным образом. Например, если

u*(w) = au(w) + b,   а > 0,

то соотношение

Е[u(Х)] > Е[u(Y)]

эквивалентно соотношению

Е[u*(Х)] > Е[u*(Y)].

Таким образом, предпочтения сохраняются, если функция полезности является линейным преобразованием исходной с положительными коэффициентами. Этот факт использовался в примере, который иллюстрировался рис. 1.2.1 , где две точки выбирались произвольным образом.

3. Предположим, что функция полезности линейна и ее угол наклона положителен, т. е.

u(w) = aw + b,    a > 0.

Тогда если Е[ Х] = μ_x и E[Y] = μ_y, то

E[u(X)] = aμ_x + b > E[u(Y)] = aμ_y + b

в том и только том случае, когда μ_x > μ_y. Таким образом, для возрастающей линейной функции полезности предпочтения относительно распределений исходов упорядочены так же, как математические ожидания этих распределений. Следовательно, если функция полезности является линейной и возрастающей, то принцип ожидаемого значения для рационального экономического поведения перед лицом неопределенности не противоречит правилу ожидаемой полезности.